The Black-Scholes model might sound like something from a college math class, but it’s actually a tool that helps traders understand what an option is worth. By plugging in some different values, the model gives a “fair price” for an option. Here’s a breakdown of how it works – and, yes, we’ll even include the famous formula. 

What is the Black-Scholes Model? 

The Black-Scholes model is a formula used to estimate the price of an option. It calculates this price by looking at key factors like time left until expiration, stock volatility, and the risk-free interest rate. When traders talk about “pricing an option,” they’re often using a variation of Black-Scholes, even if it’s behind the scenes. 

The formula (don’t worry, you don’t have to memorize It) 

The Black-Scholes formula to price a call option looks like this: 

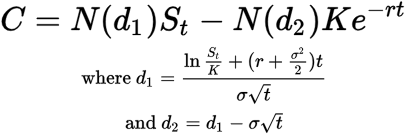
This is a theoretical model and actual results may vary

This formula estimates the “fair value” of a call option by using key inputs like stock price, strike price, time to expiration, volatility, and interest rates. Each element captures an aspect of option pricing. 

Side note: Black-Scholes is only for European options, not American ones. European options can only be exercised at expiration (not before), which makes the Black-Scholes math simpler. Also, most traders and investment firms have spreadsheets to calculate options prices – they don’t do it by hand. 

How each “Greek” fits into the model 

If you’ve read about the “Greeks” in options trading, you might be wondering how these fit into the Black-Scholes model. Well, each Greek is derived from the formula based on how option prices react to changes in different factors. Here’s how that works for each Greek: 

Delta measures how sensitive the option’s price is to a change in the stock price. In Black-Scholes, Delta increases as the option moves “in the money.” A higher Delta means the option price will react more to the stock’s moves. 

Gamma tracks the speed of Delta. In the Black-Scholes model, Gamma increases as the option gets close to the strike price. It’s highest when the option is at-the-money, which means it’s close to the strike and very sensitive to price changes. 

Theta represents time decay, which eats away at an option’s value as expiration approaches. Black-Scholes factors in time, so the closer an option is to expiration, the faster it loses value. 

Vega measures how much the option price will change with a shift in volatility. Since Black-Scholes assumes a constant volatility, it’s Vega that lets traders see how sensitive the option price is to any changes in the stock’s volatility. 

Rho tells us how sensitive the option is to interest rates. Black-Scholes uses a risk-free interest rate, so any change here can impact the option price, especially for longer-term options. 

Why Black-Scholes matters for traders 

The Black-Scholes model is the gold standard for pricing options. Knowing the theoretical value helps traders gauge if an option is cheap, pricey, or fairly valued.  

For example, if the market price of an option is above the Black-Scholes estimate, you might think it’s overpriced – and look to sell the option. On the flip side, if it’s below the estimated price, it might be a bargain buy. 

Limitations of Black-Scholes 

While many traders use the model, it’s not perfect. The model makes a few assumptions that don’t always hold up in real life: 

• Constant volatility: Markets are rarely stable, and volatility can shift suddenly. 
• No dividends: The model doesn’t account for dividends, which affect stock prices. 
• Efficient markets: Black-Scholes assumes that markets move logically, but we all know emotions can play a big role in stock price moves. 

Final thoughts: a model, not a magic wand 

Black-Scholes gives traders a starting point for pricing options. It’s not an exact science, and real-world factors can throw off the calculations. But if you understand the basics of Black-Scholes, you’ll have a better sense of how each Greek affects the value of an option – without needing a calculator. 

Key takeaways 

• The Black-Scholes model helps traders gauge the “fair value” of an option. It’s the gold-standard of options pricing, based on factors like stock price, time, volatility, and interest rates. 
• Each “Greek” plays a unique role in how an option’s price changes, helping traders understand risk and potential movement. 
• While many traders use the model, it has limits (like assuming constant volatility and ignoring dividends). It’s not perfect.